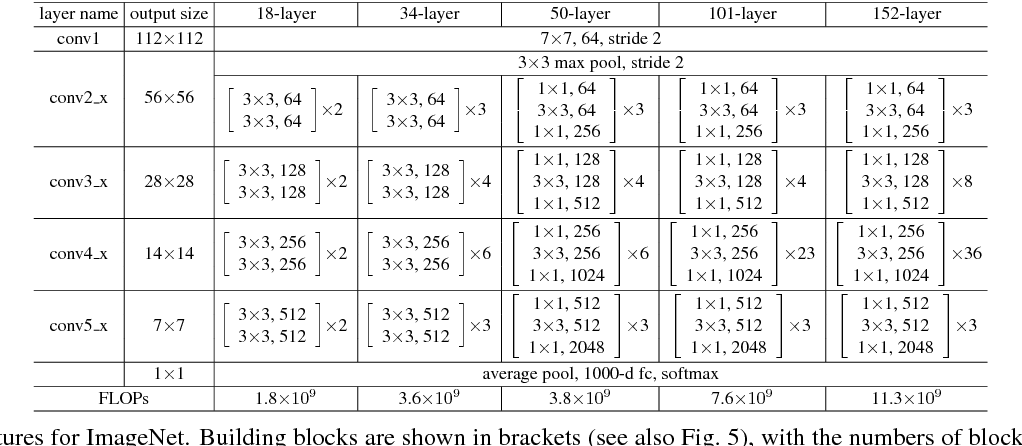
ResNet

#

This is a Pytorch implementation of the Deep Residual Learning for Image Recognition paper.

The researchers behind ResNet aimed to address the common “degradation problem” encountered in deep convolutional networks.

When the depth of a CNN model is increased, it initially shows an improvement in performance but eventually degrades rapidly as the training accuracy plateus or even worsens over time.

The common misconception is that this rapid degradation in accuracy is caused by overfitting. While overfitting due to exploding/vanishing gradients is expected in very deep networks, it is accounted for by nomalized initializations of the dataset and the intermediate Batch Normalization layers.

The degradation is definitely not caused by overfitting, as adding more layers actually causes the training error to increase. While the researchers in the paper are not sure, their conclusion is that “deep plain nets may have exponentially low convergence rates,” which can be prevented with Residual Learning.

Accompanying blog post

import torch
import torch.nn as nn
from torchinfo import summary

#

Residual Learning (no bottleneck)

#

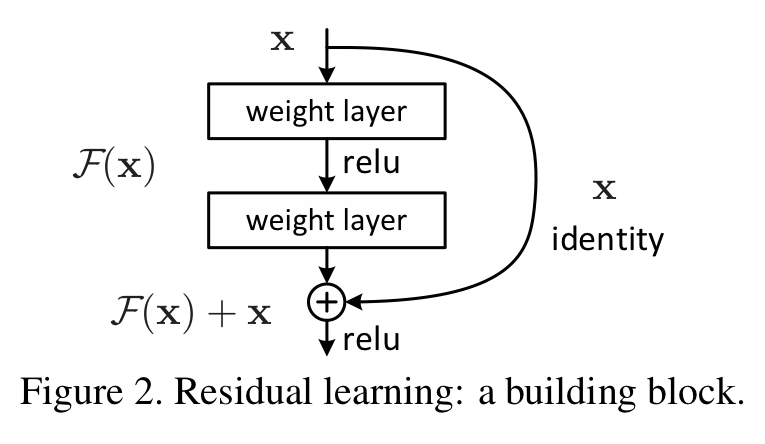
$$H(x) := F(x) + x$$

If we let $x$ be the incoming feature, the $F(x)$ is the normal weighted layers that CNNs have (Convolutional, Batch Normalization, ReLU layers). The original $x$ is then added (element-wise addition) to $F(x)$ to produce $H(x)$.

Essentially, the original features are added to the result of the weighted layers, and this whole process is one residual block. The idea is that, in the worst case scenario where $F(x)$ produces a useless tensor filled with 0s, the identity will be added back in to pass on a useful feature to the next block.

As this is a CNN model, downsampling is necessary. The issue is that the dimensions of $F(x)$ and $x$ would be different after downsampling. In such cases, the $F(x)$ and $W_ix$ are added together, where the square matrix $W_i$ is used to match dimensions.

class ResidualBlockNoBottleneck(nn.Module):
    expansion = 1

#

Parameters

input_channels: input number of channels
output_channels: output number of channels stride: the stride length of the F(x). Stride is 1 when repeating the same residual block and 2 when downsampling is used to transition to the next block. The shortcut connection will use the same stride to keep the dimensions the same.

    def __init__(self, input_channels, output_channels, stride=1):

#

No bottleneck used here.

        super(ResidualBlockNoBottleneck, self).__init__()
        self.expansion = 1

#

        self.block = nn.Sequential(

#

$3 \times 3$ convolution that maps to output_channels

            nn.Conv2d(in_channels=input_channels, out_channels=output_channels, kernel_size=3, stride=stride, padding=1, bias=False),

#

Batch normalization

            nn.BatchNorm2d(output_channels),

#

ReLU

            nn.ReLU(),

#

Another $3 \times 3$ convolution layer

            nn.Conv2d(in_channels=output_channels, out_channels=output_channels, kernel_size=3, stride=1, padding=1, bias=False),

#

Second batch normalization

            nn.BatchNorm2d(output_channels)
        )

#

ReLU

        self.relu = nn.ReLU()
        
        if stride != 1:

#

If F(x) and x are different dimensions (stride is not 1), W_i from the shortcut connection maps the number of channels in x (input_channels) to the output_channels using a $1 \times 1$ convolution to keep the width and height the same.

            self.shortcut = nn.Sequential(
                nn.Conv2d(in_channels=input_channels, out_channels=output_channels, kernel_size=1, stride=2, padding=0),
                nn.BatchNorm2d(output_channels)
            )
        else:

#

If stride is 1, x and F(x) have the same dimensions, meaning they can be added together.

            self.shortcut = nn.Sequential()

#

    def forward(self, x):
        z = self.block(x)
        z += self.shortcut(x)
        z = self.relu(z)
        return z

#

Residual Block with Bottleneck

#

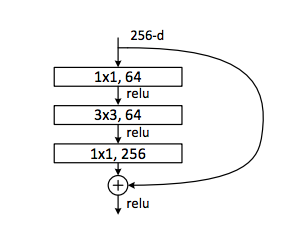
A bottleneck residual block is a variant of the residual block that uses $1 \times 1$ convolutions to create a “bottleneck.” The primary purpose of a bottleneck is to reduce the number for parameters in the network.

By utilizing a $1 \times 1$ convolution, the network first reduces the number of channels before applying the subsequent $3 \times 3$ convolution. The output is then restored to the original channel length by another $1 \times 1$ convolution. Hence, the $3 \times 3$ convolution operates on lower dimensional data.

The reduction in the number of channels leads to a significant reduction in the number of parameters in the network. This parameter reduction allows for more efficient training and enables the use of deeper and more complex architectures while managing computational resources effectively.

class ResidualBlockBottleneck(nn.Module):

#

Reduce and expand the number of channels in the bottleneck by expansion = 4.

    expansion = 4

#

Parameters

input_channels: input number of channels
output_channels: output number of channels stride: the stride length of the F(x). Stride is 1 when repeating the same residual block and 2 when downsampling is used to transition to the next block. The shortcut connection will use the same stride to keep the dimensions the same.

    def __init__(self, input_channels, in_channels, stride=1):

#

        super(ResidualBlockBottleneck, self).__init__()

        self.block = nn.Sequential(

#

$1 \times 1$ convolutional layer to map channel length to in_channels.

            nn.Conv2d(in_channels=input_channels, out_channels=in_channels, kernel_size=1, stride=1, padding=0, bias=False),

#

First batch normalization

            nn.BatchNorm2d(in_channels),

#

ReLU

            nn.ReLU(),

#

$3 \times 3$ convolutional layer to learn features

            nn.Conv2d(in_channels=in_channels, out_channels=in_channels, kernel_size=3, stride=stride, padding=1, bias=False),

#

Second batch normalization

            nn.BatchNorm2d(in_channels),

#

ReLU

            nn.ReLU(),

#

$1 \times 1$ convolutional layer to restore number of channels to in_channels*self.expansion

            nn.Conv2d(in_channels=in_channels, out_channels=in_channels*self.expansion, kernel_size=1, stride=1, padding=0, bias=False),

#

Final batch normalization

            nn.BatchNorm2d(in_channels*4)
        )

#

Final ReLU

        self.relu = nn.ReLU()
        
        if stride != 1 or input_channels != self.expansion*in_channels:

#

If F(x) and x are different dimensions (stride is not 1), W_i from the shortcut connection maps the number of channels in x (input_channels) to the output_channels using a $1 \times 1$ convolution to keep the width and height the same.

Additionally, if the input_channels is not equal to self.expansion*in_channels, the output channel length, then use a $1 \times 1$ convolution to equalize number of channels.

            self.shortcut = nn.Sequential(
                nn.Conv2d(in_channels=input_channels, out_channels=in_channels*self.expansion, kernel_size=1, stride=stride, padding=0, bias=False),
                nn.BatchNorm2d(in_channels*self.expansion)
            )
            
        else:

#

If x and F(x) have the same dimensions, add them together.

            self.shortcut = nn.Sequential()

#

    def forward(self, x):
        z = self.block(x)
        z += self.shortcut(x)
        z = self.relu(z)
        return z

#

ResNet Model

#

This is the main part of the ResNet model.

#

class ResNet(nn.Module):

#

Parameters

architecture: List of int, where each int is the repetition number for each residual block
input_width: the width of the input image
output_num: the number of classes
block_type: ResidualBlockNoBottleneck or ResidualBottleneck

    def __init__(self, architecture, input_width, output_num,  block_type=ResidualBlockNoBottleneck, input_channels=3):

#

        super(ResNet, self).__init__()
        self.architecture = architecture
        self.input_width = input_width
        self.output_num = output_num

#

The preliminary layer of Conv2d -> Batch Normalization -> ReLU. The resulting number of channels is 64, as specified by the paper.

        self.preliminary = nn.Sequential(
            nn.Conv2d(in_channels=input_channels, out_channels=64, kernel_size=7, stride=2, padding=3, bias=False),
            nn.BatchNorm2d(64),
            nn.ReLU()
        )

#

First MaxPool

        self.maxpool1 = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        self.current_channels = 64

#

Residual layers 1 ~ 4

        self.layer1 = self.make_layer(block_type, 64, self.architecture[0])
        self.layer2 = self.make_layer(block_type, 128, self.architecture[1], 2)
        self.layer3 = self.make_layer(block_type, 256, self.architecture[2], 2)
        self.layer4 = self.make_layer(block_type, 512, self.architecture[3], 2)

#

The final layer of Flatten -> FC -> Softmax. There are 5 MaxPool layers in the network, so the input_width entered in the beginning is halved five times (so divided by 32 overall). The final residual block returns self.current_channels number of channels, meaning that the output result would be (batch_size,self.current_channels, input_height // 32, input_width // 32). We are assuming that the input images are squares.

Once the result passes through the nn.Flatten() layer, the dimension of the output is be $(batch size, current channels \cdot (\frac{input width}{32})^2)$.

The dimensions of the FC layer is $(current channels \cdot (\frac{input width}{32})^2, output num)$.

        self.final = nn.Sequential(
            nn.Flatten(),
            nn.Linear(in_features=self.current_channels*int(input_width/(2**5))**2, out_features=output_num),
            nn.Softmax(dim=1)
        )

#

Propagate

    def forward(self,x):
        z = self.preliminary(x)
        z = self.maxpool1(z)
        
        z = self.layer1(z)
        z = self.layer2(z)
        z = self.layer3(z)
        z = self.layer4(z)

        z = self.final(z)
        return z

#

Create a singular block.

Parameters

block_type: ResidualBlockNoBottleneck or ResidualBlockBottleneck in_channels: reduced number of channels for bottleneck repetition_num: number of times the residual block is repeated in the layer stride: stride of the convolutional layers

Returns

nn.Sequential(*layers): Sequence of layers in the whole residual block

    def make_layer(self, block_type, in_channels, repetition_num, stride=1):

#

        layers = []
        for _ in range(repetition_num):
            layers.append(block_type(self.current_channels, in_channels, stride=stride))
            self.current_channels = in_channels*block_type.expansion

#

Only the first residual block uses stride of 2 to downsample.

            stride = 1
        return nn.Sequential(*layers)

#

Tensor Test

if __name__ == "__main__":

#

Testing the No Bottleneck Residual Block

    testing_residual_block_input = torch.randn(1,64,56,56)
    testing_residual_block = ResidualBlockNoBottleneck(64, 64, stride=2)

#

Size output: (1, 64, 28, 28)

    print(testing_residual_block(testing_residual_block_input).size())

#

Testing the Bottleneck Residual Block

    testing_residual_block = ResidualBlockBottleneck(64, 64, stride=2)

#

Size output: (1, 256, 28, 28)

    print(testing_residual_block(testing_residual_block_input).size())

#

Sample tensor simulating one training instance from ImageNet

    img = torch.randn(1,3,224,224)

#

Testing ResNet

    test_model = ResNet([3,4,6,3],224,10, ResidualBlockBottleneck)

#

Size output: (1, 10)

    print(test_model(img).size())