SE-Net
This is a Pytorch implementation of the Squeeze-and-Excitations Networks paper.

Squeeze-and-Excitation Networks, SE-Nets for short, are convolutional blocks that can be added to other models, like ResNet or VGG. The key problem that the authors of the paper wants to address is the problem of implicit and local channel dependencies.
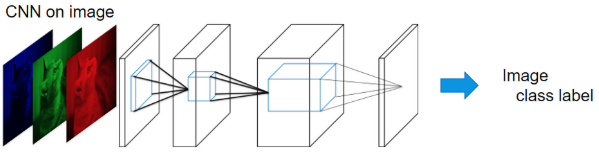
In a normal convolution like the image above, channel dependencies are implicitly included in the outputs of the convolutional layers. In other words, each layer calculates the convolution on all the channels of a local region every step.
Due to the localness of the convolutions, each channel in the output contains implicit channel embeddings tangled with local spatial correlations. To simplify further, each pixel in a channel contains the channel embeddings of the local region on the convolution was calculated on.
By incorporating the SE blocks into the model, the network can adaptively recalibrate its feature maps to capture more discriminative information, leading to improved performance.
import torch
import torch.nn as nn
from torchinfo import summarySE-Net
class se_block(nn.Module):Parameters
input_channels: input number of channels
reduction_ratio: the FC layer reduction ratio for bottleneck purposes
def __init__(self, input_channels, reduction_ratio): super(se_block,self).__init__()
self.sequence = nn.Sequential(1. Squeeze
The network first “squeezes” the outputs of the previous convolutional layer into
(batch_size, input_channels, 1, 1) shape using Global Average Pool.
nn.AdaptiveAvgPool2d((1,1)),Flatten the output to (batch_size, input_channels)
nn.Flatten(),2. Excitation
The network performs “excitation” by performing two Fully Connected (FC) layers.
The first FC layer reduces the number of channels by applying a reduction ratio. This reduction
helps in reducing the computational complexity of the SE block. The second FC layer then
expands the number of channels back to the original number. These FC layers capture the
channel dependencies and learn channel-wise relationships based on the aggregated information
from the squeeze operation.
First FC layer (output size: (batch_size, input_channels // reduction_ratio))
nn.Linear(input_channels, input_channels // reduction_ratio, bias=False), # output: bxC/rReLU
nn.ReLU(),Second FC layer (output size: (batch_size, input_channels))
nn.Linear(input_channels // reduction_ratio, input_channels),Sigmoid
nn.Sigmoid(),Unflatten layer (output size: (batch_size, input_channels, 1, 1))
nn.Unflatten(1, (input_channels,1,1)) # output: bxCx1x1
) def forward(self,x):
z = self.sequence(x)3. Rescale
Rescale by performing channel-wise multiplication (output size: (batch_size, input_channels, input_width, input_height))
z = x*z
return zTensor Test
if __name__ == "__main__":Sample tensor simulating one training instance from ImageNet
test = torch.rand(1,3,224,224)A singular SE block
model = se_block(3, 16)Size output: (1, 3, 224, 224)
print(model(test).size())