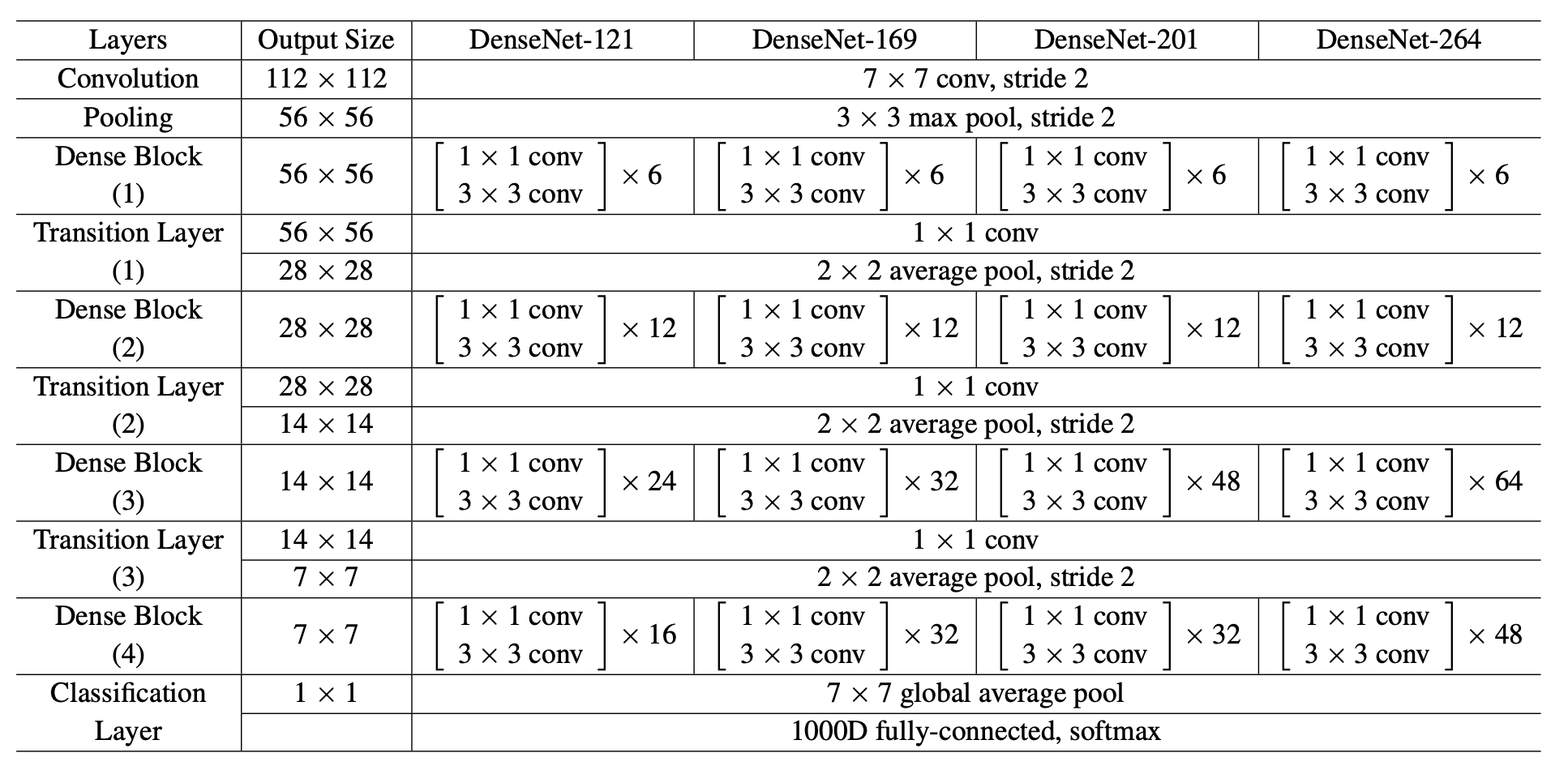
DenseNet

#

This is a Pytorch implementation of the Densely Connected Convolutional Networks paper.

The researchers behind DenseNet improve upon Residual Networks by implementing shortcut connections between every layer in the Dense Block.

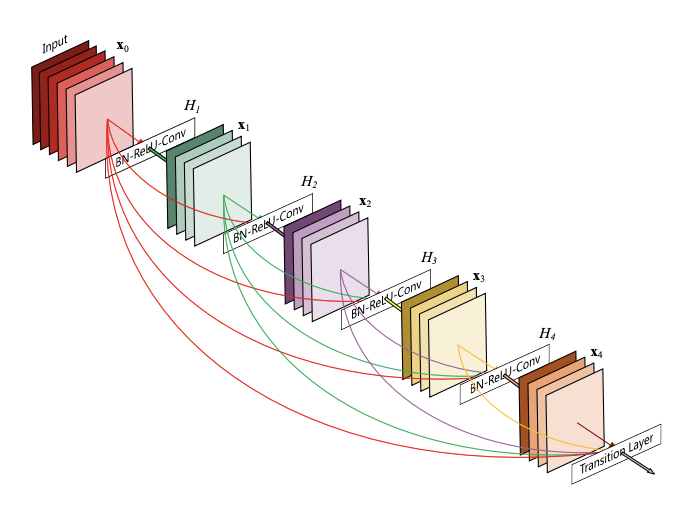
The idea is to concatenate the feature maps of all the preceding layers with the result of the current layer instead of performing element-wise addition like ResNet. The authors argue that the element-wise summation used in Residual Networks may actually impede the flow of information and emperically prove that DenseNets perform better overall.

The concatenation can be represented as

$$x_l = H_l([x_0,x_1,\dots,x_{l-1}]).$$

The feature map of layer $l$ will return $x_l$, which is the result of convolutions of the concatenations of all previous layers. The next layer will then perform convolutions on $[x_0,x_1,\dots,x_{l-1},x_{l}]$

Accompanying blog post

import torch
import torch.nn as nn
from torchinfo import summary

#

A Dense Layer

#

A dense layer contains convolutional operations and a single concatenation. Several dense layers make up a dense block.

class DenseLayer(nn.Module):

#

Parameters

input_channels: input number of channels
growth_rate: the growth rate of the dense network (number of output channels per dense layer)

    def __init__(self, input_channels, growth_rate):

#

        super(DenseLayer, self).__init__()
        self.growth_rate = growth_rate

        self.layer = nn.Sequential(

#

First batch normalization

            nn.BatchNorm2d(input_channels),

#

First ReLU

            nn.ReLU(),

#

$1 \times 1$ convolutional layer to apply bottleneck (expansion set at 4)

            nn.Conv2d(in_channels=input_channels, out_channels=4*input_channels, kernel_size=1, stride=1, padding=0, bias=False),

#

Second batch normalization

            nn.BatchNorm2d(4*input_channels),

#

Second ReLU

            nn.ReLU(),

#

$3 \times 3$ convolutional layer that maps number of channels to the growth_rate. Because each dense layer maps outputs of growth_rate number of channels, each concatenation increases the channel length by growth_rate amount, hence the name.

            nn.Conv2d(in_channels=4*input_channels, out_channels=growth_rate, kernel_size=3, stride=1, padding=1, bias=False)
        )

#

Propagate

    def forward(self,x):
        z = self.layer(x)

#

Concatenate the output and the input along the y-axis (1)

        z = torch.cat([z, x], 1)
        return z

#

Transition Layer

#

To prevent the model from having an overly large number of channels, DenseNet performs compression via Transition Layers.

Assuming a dense block returns $m$ feature maps, the transition layer performs compression to $\lfloor \theta m \rfloor$ feature maps. When $\theta = 1$, the number of feature maps remain unchanged.

The authors of the paper use $\theta = 0.5$ in their experiments.

class TransitionLayer(nn.Module):

#

Parameters

input_channels: input number of channels
theta: compression parameter

    def __init__(self, input_channels, theta=0.5):

#

        super(TransitionLayer, self).__init__()

#

self.input_channels == m

        self.input_channels = input_channels

#

Compressed number of feature maps

        self.output_channels = int(input_channels*theta)

        self.layer = nn.Sequential(

#

Batch normalization

            nn.BatchNorm2d(self.input_channels),

#

$1 \times 1$ convolution to map number of feature maps to m

            nn.Conv2d(in_channels=self.input_channels, out_channels=self.output_channels, kernel_size=1, stride=1, padding=0, bias=False),

#

Average Pool to halve input width and height

            nn.AvgPool2d(kernel_size=2, stride=2, padding=0)
        )

#

Propagate

    def forward(self,x):
        return self.layer(x)

#

Return the output number of channels

    def output_channels_num(self):
        return self.output_channels

#

DenseNet Model

#

This is the main part of the DenseNet model.

#

class DenseNet(nn.Module):

#

Parameters

architecture: List of int, where each int represents how many times to repeat a dense layer for each block
input_width: the width of the input image
output_num: the number of classes
growth_rate: the growth rate of number of feature maps

    def __init__(self, architecture, input_width, output_num, growth_rate=32):

#

        super(DenseNet, self).__init__()
        self.architecture = architecture
        self.input_width = input_width
        self.output_num = output_num
        self.growth_rate = growth_rate

#

The preliminary layer of Conv2d -> Batch Normalization -> ReLU -> Max Pool. The resulting number of channels is double the growth rate.

        self.initial = nn.Sequential(
            nn.Conv2d(in_channels=3, out_channels=self.growth_rate*2, kernel_size=7, stride=2, padding=3, bias=False),
            nn.BatchNorm2d(self.growth_rate*2),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        )

#

Dense Blocks
input_channels keeps track of the number of feature maps

        input_channels = self.growth_rate*2

#

First dense block

        self.dense_block1, input_channels = self.create_dense_block(input_channels, architecture[0])

#

First transition layer

        self.transition_layer1 = TransitionLayer(input_channels)

#

Update number of feature maps

        input_channels = self.transition_layer1.output_channels_num()

#

Second dense block

        self.dense_block2, input_channels = self.create_dense_block(input_channels, architecture[1])

#

Second transition layer

        self.transition_layer2 = TransitionLayer(input_channels)

#

Update number of feature maps

        input_channels = self.transition_layer2.output_channels_num()

#

Third dense block

        self.dense_block3, input_channels = self.create_dense_block(input_channels, architecture[2])

#

Third transition layer

        self.transition_layer3 = TransitionLayer(input_channels)

#

Update number of feature maps

        input_channels = self.transition_layer3.output_channels_num()

#

Fourth dense block

        self.dense_block4, input_channels = self.create_dense_block(input_channels, architecture[3])

#

Classification layer consisting of Avg Pool -> Flatten -> FC -> Softmax

        self.avgpool = nn.AvgPool2d(kernel_size=int(input_width/(2**5)))
        self.flatten = nn.Flatten()
        self.fc = nn.Linear(in_features=1*1*input_channels, out_features=output_num, bias=False)
        self.softmax = nn.Softmax(dim=1)

#

Propagate

    def forward(self, x):
        z = self.initial(x)
        z = self.dense_block1(z)
        z = self.transition_layer1(z)

        z = self.dense_block2(z)
        z = self.transition_layer2(z)

        z = self.dense_block3(z)
        z = self.transition_layer3(z)

        z = self.dense_block4(z)
        z = self.avgpool(z)
        z = self.flatten(z)
        z = self.fc(z)
        return self.softmax(z)

#

Create a dense block

    def create_dense_block(self, input_channels, repetition_num):

#

Parameters

input_channels: number of input feature maps
repetition_num: number of times to repeat the dense layer

Return

nn.Sequential(*layers): Sequence of layers in the whole residual block
in_channels: number of output channels

        layers = []
        in_channels = input_channels
        for _ in range(repetition_num):
            layers.append(DenseLayer(in_channels, self.growth_rate))

#

For each iteration, the number of channels increase by growth_rate amount

            in_channels += self.growth_rate
        
        return nn.Sequential(*layers), in_channels

#

Tensor Test

if __name__ == "__main__":

#

Sample tensor simulating one training instance from ImageNet

    test = torch.rand(1,3,224,224)

#

DenseNet-121

    model = DenseNet([6,12,24,16],224,1000)

#

Size output: (1,1000)

    print(model(test).size())